Design matrix

In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model.[1][2] It can contain indicator variables (ones and zeros) that indicate group membership in an ANOVA.

The design matrix represents the independent variables in statistical models which describe observed data (often called dependent variables) in terms of other known variables (explanatory variables). The theory relating to such models makes substantial use of matrix manipulations involving the design matrix: see for example linear regression. A notable feature of the concept of a design matrix is that it is able to represent a number of different experimental designs and statistical models, e.g., ANOVA, ANCOVA, and linear regression.

Contents

Example

One-way ANOVA

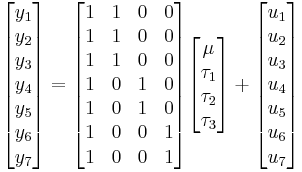
Example with a one-way analysis of variance (ANOVA) with 3 groups and 7 observations. The first column in the design matrix models the grand [global] mean of the ys, while the 3 remaining columns indicate the group membership of each observation. Here the first group consists of the 3 first observations and the next two groups each consist of two observations.

\begin{bmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \\ y_7 \end{bmatrix} = \begin{bmatrix}1 & 1 &0 &0 \\1 &1 &0 &0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix}\mu \\ \tau_1 \\ \tau_2 \\ \tau_3 \end{bmatrix} %2B \begin{bmatrix}u_1 \\ u_2 \\ u_3 \\ u_4 \\ u_5 \\ u_6 \\ u_7 \end{bmatrix}

See also

References

  1. ^ Everitt,B.S. (2002) Cambridge Dictionary of Statistics, CUP. ISBN 0-521-91099-x
  2. ^ Box, G.E.P., Tiao, G.C. (1973) Bayesian Inference in Statistical Analysis, Wiley. ISBN 0-471-57427-7 (Section 8.1.1)